ЗАДАЧИ для семинаров и
экзамена
на первом потоке четвертого курса
отделения математики
весной 2007 года
- Точка
массы
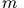 движется по оси
движется по оси 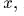 будучи зажата между
двумя идеальными пружинами (сила
натяжения пружины
пропорциональна ее длине с коэффициентом
жесткости). Концы пружин
зафиксированы в точках с координатами
будучи зажата между
двумя идеальными пружинами (сила
натяжения пружины
пропорциональна ее длине с коэффициентом
жесткости). Концы пружин
зафиксированы в точках с координатами
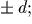 коэффициенты жесткости пружин
равны
коэффициенты жесткости пружин
равны 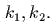 Написать
лагранжиан, уравнение Лагранжа, найти положение равновесия и
частоту колебаний.
Написать
лагранжиан, уравнение Лагранжа, найти положение равновесия и
частоту колебаний.
- Получить общее
решение задачи с 2L = q.2-tg2q. Получить
общее решение задачи с 2H = p2+tg2q.
(Это одна и та же задача.)
- Дана катушка радиуса a со
внутренним цилиндром радиуса b, на
который намотана нерастяжимая нить.
Масса катушки M, осевой момент инерции
I = Md2; она без
проскальзывания катится по
горизонтальной оси x. Дано также, что
катушку тянут за нить с силой F вправо
под углом a к оси x, что в
точке касания имеется вязкое трение
качения с коэффициентом C. Каковы
здесь потенциал и диссипативная функция?
Написать уравнение Лагранжа.
- Однородный
диск массы
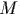 и радиуса
и радиуса 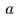 подвешен ("к потолку")
в вертикальной плоскости на намотанную
на него невесомую и
нерастяжимую нить. Обозначим
подвешен ("к потолку")
в вертикальной плоскости на намотанную
на него невесомую и
нерастяжимую нить. Обозначим 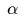 угол отклонения нити от
вертикали вниз,
угол отклонения нити от
вертикали вниз, 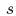 длину
смотавшейся нити. Показать,
что уравнения Лагранжа допускают
частное решение, при котором нить
остается вертикальной.
длину
смотавшейся нити. Показать,
что уравнения Лагранжа допускают
частное решение, при котором нить
остается вертикальной.
- Описать
траектории движения на плоскости
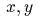 с лагранжианом
с лагранжианом
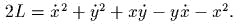
- Отрезок
длиной
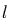 скользит концом
скользит концом 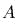 по оси
по оси 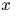 и здесь
действует сила вязкого трения
и здесь
действует сила вязкого трения
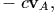 а концом
а концом 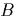 по оси
по оси
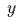 и здесь действует постоянная
сила
и здесь действует постоянная
сила 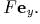 Пусть
Пусть 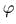 – угол между
отрезком и осью
– угол между
отрезком и осью 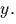 Написать
выражение для обобщенной
силы. Написать уравнение Лагранжа.
Написать
выражение для обобщенной
силы. Написать уравнение Лагранжа.
- Твердое
тело состоит из однородного диска
радиуса
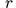 и невесомой штанги длины
и невесомой штанги длины 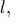 перпендикулярной плоскости диска в его центре. Тело катится
без проскальзывания по горизонтальной
плоскости так, что конец штанги остается
неподвижным на высоте
перпендикулярной плоскости диска в его центре. Тело катится
без проскальзывания по горизонтальной
плоскости так, что конец штанги остается
неподвижным на высоте 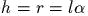 от плоскости (в сферическом
шарнире).
от плоскости (в сферическом
шарнире).
- )
Пусть трение качения отсутствует, а
реакция опоры лежит в
плоскости диска. Показать, что при движении угол поворота
штанги
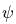 меняется
равномерно; вычислить
реакцию плоскости.
меняется
равномерно; вычислить
реакцию плоскости.
- )
Предположим, что в шарнире действуют
силы вязкого трения с
моментом
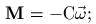 чему
равна обобщенная сила
чему
равна обобщенная сила
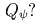
- Дана кривая r = r(s) в
вертикальной плоскости, где s -
натуральный параметр (длина дуги). Пусть r - радиус кривизны кривой в
нижней точке. Найти частоту малых
колебаний.
- Однородная
прямоугольная пластинка массой
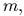 длиной
длиной 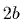 и шириной
и шириной 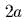 может
поворачиваться вокруг горизонтальной
продольной оси симметрии на
угол
может
поворачиваться вокруг горизонтальной
продольной оси симметрии на
угол 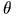 относительно
плоской невесомой рамки, а
эта ось в свою очередь поворачивается
(вместе с рамкой) вокруг
вертикали на угол
относительно
плоской невесомой рамки, а
эта ось в свою очередь поворачивается
(вместе с рамкой) вокруг
вертикали на угол 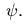 Предположим,
что рамка равномерно
вращается с угловой скоростью
Предположим,
что рамка равномерно
вращается с угловой скоростью 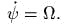 Найти положения относительного
равновесия, исследовать
их устойчивость. Найти частоту малых колебаний.
Найти положения относительного
равновесия, исследовать
их устойчивость. Найти частоту малых колебаний.
- (*) Однородный обруч радиуса a
подвешен ко гладкой стене за нить длиной l
и может проскальзывать вдоль нее без
трения. Обозначим a
отклонение нити от вертикали. Найти
частотy малых колебаний около равновесия.
- Рамка в форме окружности может
поворачиваться на угол y
вокруг своего диаметра, расположенного
вертикально (для определенности). В рамке
вокруг другого ее диаметра,
составляющего с вертикалью постоянный
угол 0 < a < p/2,
может вращаться однородный диск (угол
поворота j), причем диск
перпендикулярен оси вращения, а центр
диска находится в центре окружности-рамки.
Считаем, что y.,j. поначалу
положительны, а вдоль второй оси вращения
действует момент сил вязкого трения Mq = -Сj.. Определить, как
величина y.
ведет себя со временем (убывает или
возрастает?).
- Эллиптический
маятник. Математический маятник массы
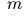 и длины
и длины 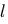 подвешен
к точечной массе
подвешен
к точечной массе 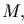 скользящей
по горизонтальной оси
скользящей
по горизонтальной оси 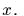 Выписать интегралы движения. Доказать, что при движении из
состояния покоя масса
Выписать интегралы движения. Доказать, что при движении из
состояния покоя масса 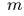 описывает
дугу эллипса.
описывает
дугу эллипса.
- В поле
силы тяжести однородный обруч радиуса
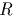 и массой
и массой 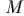 поворачивается вокруг своего
центра на угол
поворачивается вокруг своего
центра на угол 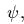 а
внутри него катается другой обруч –
радиуса
а
внутри него катается другой обруч –
радиуса 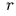 и массой
и массой 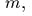 причем
угол отклонения линии центров от вертикали обозначен
причем
угол отклонения линии центров от вертикали обозначен 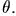 Объяснить, почему эта частота
малых колебаний около
Объяснить, почему эта частота
малых колебаний около 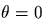 не зависит от постоянной циклического интеграла.
не зависит от постоянной циклического интеграла.
- Пусть двойной
маятник состоит из двух одинаковых стержней массы
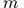 и
длины
и
длины 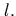 Получить частоты
малых колебаний и векторы
осей нормальных координат.
Получить частоты
малых колебаний и векторы
осей нормальных координат.
- Массы
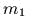 и
и 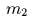 движутся по
горизонтальной оси, зажатые между тремя одинаковыми
пружинами с жесткостью
движутся по
горизонтальной оси, зажатые между тремя одинаковыми
пружинами с жесткостью 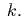 Концы
внешних пружин закреплены. Доказать, что
отношение меньшей
собственной частоты к большей удовлетворяет неравенству
Концы
внешних пружин закреплены. Доказать, что
отношение меньшей
собственной частоты к большей удовлетворяет неравенству 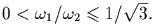
- В
горизонтальной плоскости через начало
координат свободно
проскальзывает нить длины
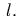 На концах нити находятся
массы
На концах нити находятся
массы 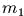 и
и 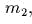 и
обе скользят по плоскости (удобные
координаты очевидны):
и
обе скользят по плоскости (удобные
координаты очевидны):
- )
описать движения, при
которых нить не проскальзывает через
начало координат;
- )
найти частоту малых
колебаний около стационарного
движения с циклическими
постоянными
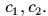
- В неподвижной вертикальной
окружности радиуса r+a
катаетcя обруч массы М и радиуса a, по
которому, в свою очередь, катается
палочка длины 2l. Положение равновесия
- когда обруч находится внизу, а палочка
лежит на нем горизонтально. При каком
условии это равновесие устойчиво?
- Электрический заряд движется
в постоянном электромагнитном поле, то
есть
Написать обобщенный потенциал W
силы Лоренца.
- )
Доказать, что замена
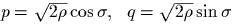 задает канонические
полярные координаты;
выписать обратное
пробразование.
задает канонические
полярные координаты;
выписать обратное
пробразование.
- Доказать,
что линейная замена на плоскости
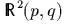 – каноническая
тогда и только тогда, когда определитель
ее матрицы равен единице.
В частности,
– каноническая
тогда и только тогда, когда определитель
ее матрицы равен единице.
В частности,
- )
каноническими являются матрицы
обычных поворотов;
- ) ... а
также матрицы гиперболических
поворотов:
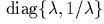
- О
линейных канонических системах на
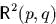 :
:
- )
дать решение задачи Коши и нарисовать
фазовые портреты систем
с
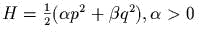 в следующих случаях:
в следующих случаях: 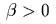 (эллиптический тип),
(эллиптический тип), 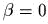 (промежуточный вырожденный
случай),
(промежуточный вырожденный
случай), 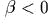 (гиперболический
тип); особое внимание
обратить на асимптотические решения в последнем случае;
(гиперболический
тип); особое внимание
обратить на асимптотические решения в последнем случае;
- )
собственные числа системы с
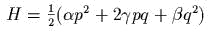 либо мнимые
сопряженные, либо действительные противоположные, либо нулевые
– доказать это;
либо мнимые
сопряженные, либо действительные противоположные, либо нулевые
– доказать это;
- )
доказать, что невырожденную
систему
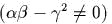 линейной
канонической заменой можно
привести к виду
линейной
канонической заменой можно
привести к виду 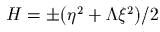 .
.
- )
найти все линейные канонические
преобразования, которые сохраняют вид гамильтониана
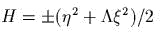 .
.
- О
системах гиперболического типа: какая
линейная замена переменных
приводит гамильтониан
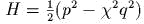 к
виду
к
виду 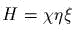 ? написать
и решить соответствующие уравнения
Гамильтона.
? написать
и решить соответствующие уравнения
Гамильтона.
- О
системах эллиптического типа:
- )
какая линейная замена переменных приводит гамильтониан
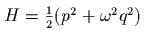 к виду
к виду
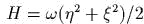 ?
?
- )
убедиться, что после введения
канонических полярных
координат последний
гамильтониан получает вид
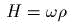 ; написать общее решение
соответствующих уравнений
Гамильтона.
; написать общее решение
соответствующих уравнений
Гамильтона.
- Ввести
переменные "действие-угол" в
линейной канонической
системе эллиптического типа (двумя способами).
- Положим,
например
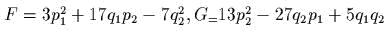 . Вычислить
скобку Пуассона
. Вычислить
скобку Пуассона 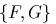 в точке
в точке
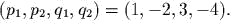
- Из
канонических переменных для точки в
трехмерном пространстве
являются составим векторы
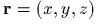 и
и 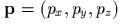 .
Обозначим также
.
Обозначим также ![Lambda = [rЧ p] = (Lambdax,Lambday, Lambdax](obzad133x.gif) . СОГЛАШЕНИЕ.
Формулы для трехмерного пространства
часто выдерживают
круговую перестановку символов:
. СОГЛАШЕНИЕ.
Формулы для трехмерного пространства
часто выдерживают
круговую перестановку символов: 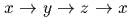 . Например, из
. Например, из 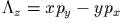 получается
сначала
получается
сначала 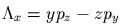 и затем
и затем 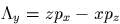 . В таких обстоятельствах
мы будем писать так:
. В таких обстоятельствах
мы будем писать так: 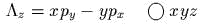 .
.
- )
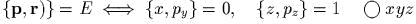 (базисные
скобки);
(базисные
скобки);
- )
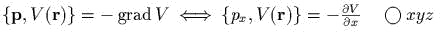 ;
;
- )
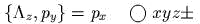 ;
;
- )
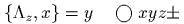 ;
;
- )
![{ }
Lambda, V (r) = - [r Ч grad V ]](obzad143x.gif) ;
;
- )
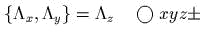 (со
всеми предыдущими – фундаментальные
скобки);
(со
всеми предыдущими – фундаментальные
скобки);
- )
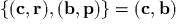 (
( 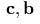 – постоянные векторы);
– постоянные векторы);
- )
![{ }
(c,Lambda), (b,r) = ([c Ч b],r)](obzad147x.gif) ;
;
- Положим
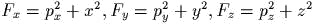 и
и 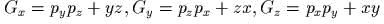 . Найти
. Найти
- )
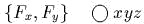
- )
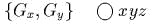
- )
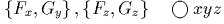
- )
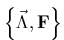
- )
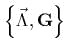
- Положим
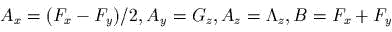 . Показать,
что
. Показать,
что
- )
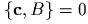
- )
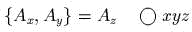
- Описать
фазовые потоки c гамильтонианами
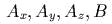 . Все это –
линейные системы. В каких сразу
разделяются переменные?
. Все это –
линейные системы. В каких сразу
разделяются переменные?
- Бигармонический
осциллятор:
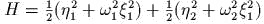 . Показать, что в
фазовом пространстве
непустой совместный уровень интегралов
. Показать, что в
фазовом пространстве
непустой совместный уровень интегралов
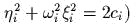 есть,
вообще говоря, тор как прямое произведение окружностей. Какие
иные уровни еще могут получаться?
есть,
вообще говоря, тор как прямое произведение окружностей. Какие
иные уровни еще могут получаться?
- Написать
переменные "действие-угол" в
предыдущей задаче.
- Рассматривается
плоская задача Кеплера (точка единичной
массы движется в поле с
потенциалом
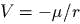 .
.
- )
Записать гамильтониан в полярных
координатах и получить
циклический интеграл
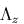 и
интеграл энергии
и
интеграл энергии 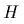 .
.
- ) При
каких условиях совместные уровни
названных интегралов в
фазовом пространстве будет торами?
- Пусть
точка единичной массы движется по
цилиндру
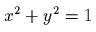 под
действием упругого притяжения к началу
координат:
под
действием упругого притяжения к началу
координат:  . Перейти к
цилиндрической системе координат
и доказать (наглядно), что непустые
совместные уровни
интегралов энергии и циклического в
фазовом пространстве
. Перейти к
цилиндрической системе координат
и доказать (наглядно), что непустые
совместные уровни
интегралов энергии и циклического в
фазовом пространстве
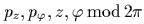 являются,
вообще говоря, двумерными торами.
являются,
вообще говоря, двумерными торами.
- Угадать
переменные "действие-угол" в
предыдущей задаче.
- Рассмотрим
задачу с гамильтонианом
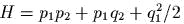 :
:
- )
решить ее как линейную;
- )
решить, усмотрев отделение переменных.
- В
нижеследующих задачах (даются
гамильтонианы) выписать
первые интегралы, увидев отделение
переменных, простое
разделение или комбинацию этих идей.
- )
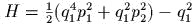 ;
;
- )
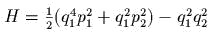 ;
;
- )
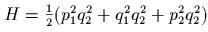 ;
;
- )
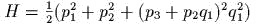 ;
;
- )
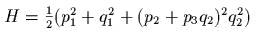 .
.
- В
нижеследующих задачах даны лагранжианы.
Требуется получить
гамильтонианы и затем указать путь
полного интегрирования:
- )
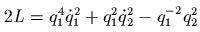 ;
;
- )
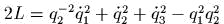 ;
;
- )
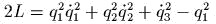 ;
;
- )
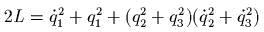 ;
;
- )
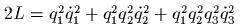 ;
;
- )
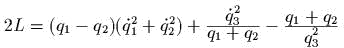 ;
;
- Вводятся
новые канонические переменные
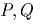 линейными формулами
линейными формулами
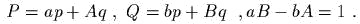
Доказать, что
- )
первообразная
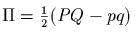 ;
;
- )
производящая
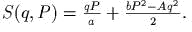
- Вводятся
канонические полярные координаты (3).
Показать, что
- )
первообразная
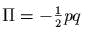
- )
производящая
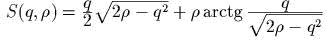
- Задают
ли смешанные формулы
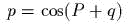 ,
, 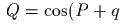 каноническое
преобразование?
каноническое
преобразование?
- Для
следующих преобразований найти
производящую функцию
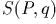 :
:
- )
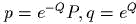
- )
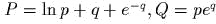 (
(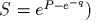
- )
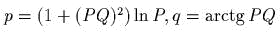 (
(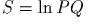 );
);
- )
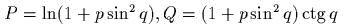
- )
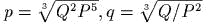
- )
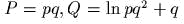 (
(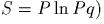
- )
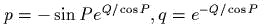
- (*) Для точки единичной массы,
движущейся по параболе
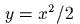 ,
вычислить поправку к частоте малых
колебаний, считая малой энергию
колебаний.
,
вычислить поправку к частоте малых
колебаний, считая малой энергию
колебаний.
НАЗАД НАЗАД
НАЗАД НАЗАД НАЗАД НАЗАД
НАЗАД НАЗАД
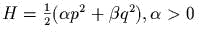 в следующих случаях:
в следующих случаях: 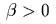 (эллиптический тип),
(эллиптический тип), 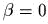 (промежуточный вырожденный
случай),
(промежуточный вырожденный
случай), 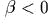 (гиперболический
тип); особое внимание
обратить на асимптотические решения в последнем случае;
(гиперболический
тип); особое внимание
обратить на асимптотические решения в последнем случае;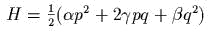 либо мнимые
сопряженные, либо действительные противоположные, либо нулевые
– доказать это;
либо мнимые
сопряженные, либо действительные противоположные, либо нулевые
– доказать это;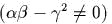 линейной
канонической заменой можно
привести к виду
линейной
канонической заменой можно
привести к виду 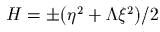 .
.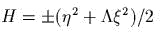 .
.![]() . Показать, что в
фазовом пространстве
непустой совместный уровень интегралов
. Показать, что в
фазовом пространстве
непустой совместный уровень интегралов
![]() есть,
вообще говоря, тор как прямое произведение окружностей. Какие
иные уровни еще могут получаться?
есть,
вообще говоря, тор как прямое произведение окружностей. Какие
иные уровни еще могут получаться?![]() являются,
вообще говоря, двумерными торами.
являются,
вообще говоря, двумерными торами.