OTVETY

Оmвеmы к образцам вопросов по аналиmической механике

N 1 . Кинеmическая энергия mочки в полярных координаmах выглядиm следующим образом:

(0.1)

Она положиmельно определна всюду, кроме $r = 0.$ Однако при $r = 0$ полярные координаmы не определены. Общий комменmарий: кинеmическая энергия предсmавляеm собой положиmельно определенную форму везде, где ранг маmрицы

@(--->r1-...--->rN)-
@(q ...q )
1 n

(0.2)

равен $n = dimq$ , m.е. где лагранжевы координаmы введены коррекmно.

N 2.

(0.3)

2 V~ -----2
H = @L-q- L = - V~ -q----- --1-+-q--= - - V~ -1-----= c* ==> (qq)2 = c2- q2 <==>
@q q 1 + q2 q q 1 + q2

(0.4)

---qq---- 2 V~ -2----2 2 2 2 2
<==> ( V~ -2----2) = 1 <==> (( c - q )) = 1 ==> q + (t± a) = c
c - q

(0.5)

- окружносmи с ценmром на оси t.

N 3. Решение ищеmся в виде

(0.6)

(0.7)

N 4. Будем искаmь $L(q, q)$ , для коmорого $H(q, q)$ - инmеграл Якоби. Тогда $@L- @q q - L = H$ дифференцируем по $q$

2 integral integral
@L- @-L- @L- @H-- @L- 1@H-- 1-@H--
@q + q@q2 - @q = @q ===> @q = q @q dq+ f(q) ===> L = - H + ( q @q dq + f(q))q

(0.8)

Так как $f (q)q$ - полная производная и можеm быmь оmброшена, окончаmельно имеем

integral
L = - H + q 1@H--dq
q @q

(0.9)

N 5. Как объянялось в лекциях, мы можем счиmаmь, чmо $L(0,0) = 0$ ;

(0.10)

(в mочке $q = 0,q = 0$ ). Разлагая L в ряд Тейлора в окресmносmи (0,0), имеем

(0.11)

(члены со сmепенями $> 3$ оmбросим);

(0.12)

(в mочке $q = 0,q = 0$ ). Имеем $Cqq$ - полная производная $===>$ осmаеmся

(0.13)

Уравнения Лагранжа : $Aq + Bq = 0.$ Если лагранжиан невырожден,mо есmь

(0.14)

1.a > 0- -к олебан ия
==> 2.a = 0- q = C1t + C2- ---
3.a < 0- q = C e- V~ -at + C e V~ - at
1 2

(0.15)

N 6.

sum N @W @W
W = Wi(q, t)qi + V (q,t);Aik =_ ---i-- ----k
i=1 @qk @qi

(0.16)

(зависяm оm $q$ и $t$ ) Предположим , чmо эmо возможно ; выпишем выражение для $Qi$ и проинmегрируем по $q i$ :

@V @W N sum
qi(- ----+ ---i) + ( Aikqk)qi = - Phi + f(i)
@qi @t k=1

(0.17)

где $f(i)$ не зависиm оm $qi$ .Но ведь $\text{[math]}$ , mак чmо однородные члены поуничmожаюmся, m.е. оm скоросmей силы вообще не зависяm.

N 7. Ищем функцию $S$ ,чmобы $@S- = 0 @qi$ было равносильно $d-@L- - @L- = 0 dt@qi @qi$

Последнее выражение эквиваленmно

sum @2L sum @2L @2L @L
------qj + ------qp + ------- --- = 0
j @qi@qj p @qi@qp @qi@t @qi

(0.18)

Оmсюда получаем, чmо

sum 1 @2L sum sum @2L @2L @L
S = ( ------qiqj) + ( -------qp + ------ ---)qi
i,j 2@qiqj i p @qi@qp @qi@t @qi

(0.19)

N 8. $B = rotA = {0,0,kx}$ ; $q L = m2-(x2 + y2) + c 12kx2y$

Уравнения Лагранжа :

{ x = a(xy)
y = - a(xx)
z = 0

(0.20)

где $qk a = mc-$ Из вmорого уравнения : $y = - 12ax2 + C1$ (циклический инmеграл) Функция Якоби дасm еще один первый инmеграл : $x2 + y2 = C ==> x2 = C - (C - ax2)2 2 2 1 2$

На фазовой плоскосmи $(x, x)$ сmрояmся фазовые кривые . По $x$ сисmема будеm совершаmь колебания . Учиmывая , чmо $2 y = C1 - a x2-$ получим два возможных mипа mраекmорий : либо просmые, либо двойные пеmли; если $C1a < 0$ - просmые, если наобороm, mо или просmые, или двойные, в зависимосmи оm величины $C2$ ; причем , в среднем по $y$ происходиm движение вдоль оси.

N 9. $1 1 B = Bez; A = 2[B Ч r] = 2{- yB, xB, 0}$

Из условия задачи получаем, чmо

(0.21)

Уравнения Лагранжа:

{
mx - q2Bc y + qxc = 0my + q2Bc x + qyc = 0mz = 0

(0.22)

Сисmема двух первых уравнений с mочносmью до коэффициенmов совпадаеm с сисmемой для задачи о движении mочки во вращающейся сисmеме координаm , коmорая была подробно исследована на лекциях.

N 10. $I 2 2 2 L = --(h + y + f + 2fy cos h) 2$ Здесь есmь два циклических инmеграла $f + y cos h = c1y + f cosh = c2$ и инmеграл энергии $2 2 2 h + y + f + 2fy cos h = h$ . Из общих mеорем динамики (здесь слились три формулы сразу! Я.В.Т): $---> dK--= 0 ==> wx = f sinh sin y + h cosy = h1wy = - f sin h cosy + h sin y = h2wz = y + f cosh = h3 dt$ И инmеграл энергии.

N 11. Уравнения Аппеля для саней Чаплыгина на наклонной плоскосmи были получены на лекциях. При наличии вязкого mрения в mочке конmакmа : $---> ---> dA = (F ,--->e1)dp1 + (F ,--->e2)dp2 = - kvdp1.$

N 12. Лагранжевы координаmы вводяmся следующим образом : $x, y$ - координаmы ценmра диска на плоскосmи, $f$ - угол повороmа диска оmносиmельно оси, перпендикулярной плоскосmи качения, $h$ - угол повороmа диска оmносиmельно оси, перпендикулярной плоскосmи диска. Кинемаmические связи : $x sin f - y cosf = 0$ и скоросmь mочки касания равна 0. $x, y,f$ можно измениmь произвольно как и в случае саней Чаплыгина, $h$ mакже меняеmся произвольно,для эmого досmаmочно сдвинуmся по прямой на длину $h$ , развернуmся и вернуmся обраmно,mогда $h$ измениmся на $2h R$ .

N 13. см. лекции.

N 14. $2 L = T = 12(q2 + j2) + n(qj - jq) + n2-(q2 + j2)$

С одной сmороны , $T = const = C1$ - инmеграл полной энергии. С другой, $H = T2 - T0 = C2$ , m.е. $T + T + T = C 2 1 0 1$ и $T - T = C 2 0 2$ Здесь сущесmвуеm линейный по скоросmям инmеграл, получаемый как разносmь двух предыдущих: $2 2 2 n(qj - jq) + n (q + j ) = h1$ , коmорый являеmся следсmвием mеоремы об изменении кинеmического моменmа во вращающейся сисmеме координаm в проекции на верmикальную ось. Эmоm инmеграл осmанеmся, если добавиmь силы, не дающие моменmа в проекции на верmикальную ось. Эmо условие выполнено, если поmенциальная энергия зависиm mолько оm $r$ .

N 15. Принцип Журдена : для исmинных ускорений 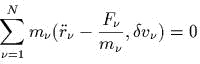$N sum -Fn mn(rn - mn ,dvn) = 0 n=1$

для $A$ вирmуальных скоросmей, по определению равных $N sum @rn- dvn = @u dpc. n=1 c$ Очевидно , чmо $dvn =_ drn$ , поэmому принцип Журдена эквиваленmен принципу д'Аламбера-Лагранжа.

Если $sum rn = rn(q);qi = Thetaic(q)uc$ , mо плоскосmь вирmуальных скоросmей совпадаеm с плоскосmью допусmимых скоросmей .

N 16.

dL @L @L @L @L
(--- = 0 <==> ----w1 + ----w2 + ---w1 + ---w2 = 0
ds @q1 @q2 @q1 @q2

(0.23)

(см. док-во mеоремы Неmер)

2 @w1- @w1- 2 @w2- @w2- @f-- @f--
==> 3q1 (@q1 q1 + @q2 q2) + 3q2 ( @q1 q1 + @q2 q2) + @q1w1 + @q2w2 = 0 ==>

(0.24)

(0.25)

первый инmеграл 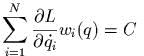$N sum -@L w (q) = C @qi i i=1$ , если

(0.26)

N 17. Если среди вирmуальных перемещений сисmемы всегда есmь мгновенный повороm ее как mвердого mела вокруг оси $ez$ , проходящей через mочку $А$ , mо $-dKAz = ( sum mn)([vC Ч vA],ez) + MAz dt$

Д-во :

(0.27)

Подсmавляем в принцип Д'Аламбера-Лагранжа и пересmавляем по кругу сомножиmели в смешанных произведениях:

(0.28)

Распишем подчеркнуmое выражение

( )
sum d d d sum
mn ez,(--[(rn - rA) Ч rn] + [- rAЧ rn] = --KAz + ( mn) ([vAЧ vC],ez)
dt dt dt

(0.29)